Services

Solution:

Step 1. Data

Organize what you know, and what you are looking for.

Given:

$m=0$ - the mass of the pulley,
$\overrightarrow{a}=0$ - the acceleration of the free end of the rope (C) relative to the Earth at the initial time $t=0$,
$\overrightarrow{a}$ - the acceleration of the free end of the rope (C1) relative to the Earth at the time t = 0+$\Delta t,$

Find:

${\overrightarrow{a}}_o$ - the acceleration of the center of the pulley relative to the Earth,

Step 2. Diagram

Let's sketch a diagram to help visualize what is going on. It is very helpful to draw two diagrams, which represent changes of object's position in some time interval $\Delta t$ (Figure 1).

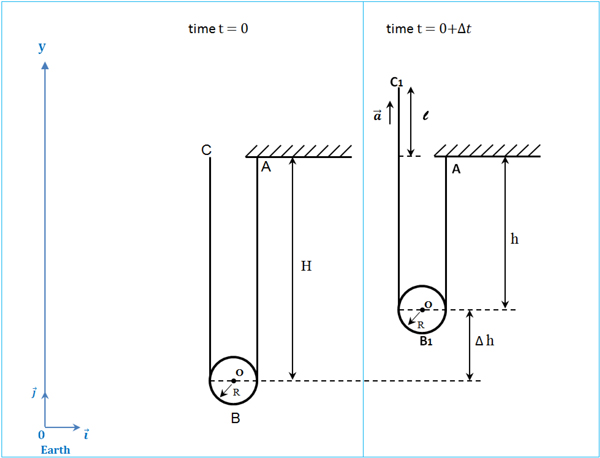
Figure 1.

Reference frame

Let us consider the motion of the pulley relative to the Earth - inertial reference frame $\overrightarrow{i}\ 0\ \overrightarrow{j}$.

Notation

$\overrightarrow{i},\ \overrightarrow{j}$ - basis vectors.
$t$ - the time
$\Delta t$ - the time change
$A$ - the point of fixing the rope to the ceiling,
$O$ - the center of rotation of the pulley
$\textrm{С}$ - the position of free end of the rope at the initial time $t=0$,
${\textrm{С}}_1$ - the position of free end of the rope at the time $t=0+\Delta t$,
$B$ - the lowest position of the rope at the initial time $t=0$,
$B_1$ - the lowest position of the rope at the time $t=0+\Delta t,$
$l$ - the length of pulled rope in the time interval $\Delta t$,
$H$ - the distance from the center of the pulley to the celling at the initial time $t=0$,
$h$ - the distance from the center of the pulley to the celling at the time $t=0+\Delta t$,
$\Delta h$ - the change of position of the center of the pulley in the time interval $\Delta t$,

Step 3. Equation

The key to this problem is to see (Figure 1.) that the full length of the rope is constant: $\left|ABC\right|=$ $\left|AB_1C_1\right|$.

$\left|ABC\right|=2\bullet H+\pi \bullet R$ at the initial time $t=0$,

$\left|AB_1C_1\right|=$ $2\bullet h+\pi \bullet R+l$ at the time t = 0+$\Delta t$, so

$\left\{\begin{array}{c} {2\bullet H+\pi \bullet R=2\bullet h+\pi \bullet R+l} \\ {H=h+\Delta h} \end{array}\right. $(1)
(2)

Solving the system of liner equations (1) and (2), we obtain

$l=2\bullet \Delta h$.

To get acceleration we have to take the second derivative of both sides $\frac{d^2l}{dt^2}=2\bullet \frac{d^2(\Delta h)}{dt^2}$. Finally, the acceleration of the center of the pulley can be expressed as twice the acceleration of free end of the rope $\left|{\overrightarrow{a}}_o\right|=2\bullet \left|\overrightarrow{a}\right|.$

Solution:

Step 1. Data

Organize what you know, and what you are looking for.

Given:

$\rho $ - the density of snow,
$d$ - the depth of snow,
$M$ - the mass of the truck,
$v_0$ - the velocity of the truck at the time $t=0$,
$F_0$ - the force between the tires and the road,
$F_0$ - constant,
$W$ - the width of cleared road

Find:

(Part a) Find a differential equation in the form of ${dv}/{dt}=f(v,\rho ,d,M,F_0)$,
(Part b) Find steady-state speed.
(Part c) Find an integral version of the equation from (Part a).

Step 2. Diagram

Let's sketch a diagram to help visualize what is going on. Find all forces involved in the given physical process. Draw free-body diagram with all relevant variables to describe the process. It is very helpful to draw two diagrams, which represent changes of object's position in some time interval $\Delta t$ (Figure 2).

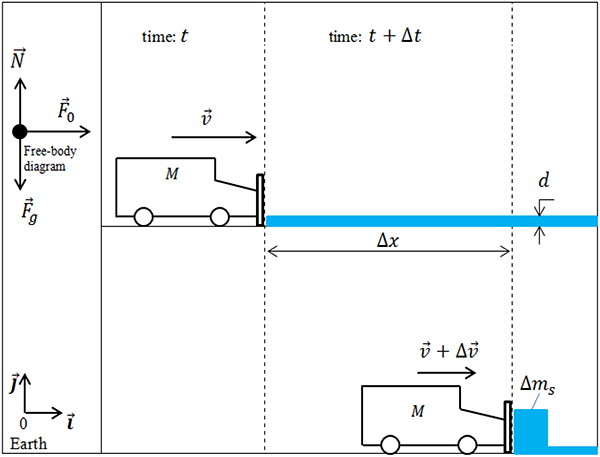
Figure 2.

Reference frame

We will consider the motion of the truck relative to the Earth - inertial reference frame $\overrightarrow{i}\ 0\ \overrightarrow{j}$.

Step 3. Equation

When starting to solve a problem, it is often not clear what forces should be taken into account and what laws can be applied. Therefore, it is useful to simplify the problem. In our case, you can replace the truck with a large, heavy ball and a snowflake - with a small light ball. Because of snowflakes are collected by the truck and then move at a speed equal to the speed of the truck, we can therefore draw an analogy with an absolutely inelastic collision of two balls. As you know, the law of conservation of energy is not applicable, but the law of conservation of momentum is applicable in the case of an absolutely inelastic collision of two balls.

The system, consisting of the truck and snow, is a closed system if there are no external forces acting on it. In our case, however, there are tree external forces (see Figure 2, Free-body diagram); gravity, normal reaction and the force ${\overrightarrow{F}}_0$ between the tires and the road:

${\overrightarrow{F}}_{net}=\sum^n_{i=0}{{\overrightarrow{F}}_i}$ - the vector sum of gravitational, normal reaction and ${\overrightarrow{F}}_0$ forces.

By the general form of Newton's second law $\frac{d\overrightarrow{P}}{dt}={\overrightarrow{F}}_{net}$, this equation can be re-arranged to read:

$d\overrightarrow{P}={\overrightarrow{F}}_{net}\bullet dt$(1)

where $\overrightarrow{P}$ is the total momentum of the closed system.

Let us consider the system change in a short time interval $\Delta t$, when the truck has picked up a small amount of snow $\Delta m_s$and has changed its velocity $\Delta \overrightarrow{v}$. Then the change in momentum of the entire system is expressed by the formula

$\overrightarrow{P}\left(t+\Delta t\right)-\overrightarrow{P}(t)={\overrightarrow{F}}_{net}\bullet \Delta t.$(2)

$\overrightarrow{P}(t)=M\overrightarrow{v}$ - the momentum of the system at time $t$,

$\overrightarrow{P}\left(t+\Delta t\right)=(M+\Delta m_s)\left(\overrightarrow{v}+\Delta \overrightarrow{v}\right)$ - the momentum of the system at time $\left(t+\Delta t\right)$.

Substituting the above expressions into equation (2), we have

$\left(M+\Delta m_s\right)\left(\overrightarrow{v}+\Delta \overrightarrow{v}\right)-M\overrightarrow{v}={\overrightarrow{F}}_{net}\bullet \Delta t$(3)

Opening parentheses, we obtain

$\ M\overrightarrow{v}+M\Delta \overrightarrow{v}+\Delta m_s\overrightarrow{v}+\Delta m_s\Delta \overrightarrow{v}-M\overrightarrow{v}={\overrightarrow{F}}_{net}\bullet \Delta t$

We now see that two like terms cancel. Also we can neglect the product $\Delta m_s\Delta \overrightarrow{v}$ because it is an infinitesimal of the second order, and the equation takes the simpler form:

$M\Delta \overrightarrow{v}+\Delta m_s\overrightarrow{v}={\overrightarrow{F}}_{net}\bullet \Delta t$(4)

Let's assume that the change in the mass of snow occurs continuously, without jumps, so that there exists a derivative $dm/dt$.

Divide both parts of equation (4) by $\Delta t$ and rewrite it in the form of limit, when $\Delta t\to 0$

${\mathop{lim}_{\Delta t\to 0} \left(M\frac{\Delta \overrightarrow{v}}{\mathit{\Delta}t}\right)\ }+\overrightarrow{v}{\mathop{lim}_{\Delta t\to 0} \left(\frac{\mathit{\Delta}m_s}{\mathit{\Delta}t}\right)\ }={\overrightarrow{F}}_{net}, $

$M\frac{d\overrightarrow{v}}{dt}+\overrightarrow{v}\frac{dm_s}{dt}={\overrightarrow{F}}_{net}$(5)

We have thus established the equation of system's motion with continuous addition of mass and with the presence of a net external force. Keep in mind that $dm_s/dt>0$.

Since the direction of the truck motion is parallel to the vector $\overrightarrow{i}$, we can write $\frac{d\overrightarrow{v}}{dt}=\frac{dv}{dt}\overrightarrow{i}$, (as $\frac{d\overrightarrow{i}}{dt}=0$) and

${\overrightarrow{F}}_{net}=F_0\bullet \overrightarrow{i}+(N-F_g)\bullet \overrightarrow{j}$, where $N=F_g$

We can now re-write equation (5) in the form of projection onto the basis vector $\overrightarrow{i}$

$M\frac{dv}{dt}\overrightarrow{i}+v\frac{dm_s}{dt}\overrightarrow{i}=F_0\bullet \overrightarrow{i}. $

Finally, the above equation can be written in scalar form as

$M\frac{dv}{dt}+v\frac{dm_s}{dt}=F_0\ $(6)

Now we want to find an expression for the mass of snow that the truck picked up at the time $t+\Delta t$ (see Figure 2)

$\Delta m_s=\rho \bullet \left(d\bullet W\bullet \Delta x\right)=\rho \bullet \left(d\bullet W\bullet v\bullet \Delta t\right).$

Considering that $\Delta t\to 0,$ we have

$dm_s=\rho \bullet \left(d\bullet W\bullet v\right)\bullet dt.$

(Part a).

Substituting the above expression into equation (6) we obtain a differential equation for the speed of the truck

$\frac{dv}{dt}=\ \frac{F_0-\rho dWv^2}{M}$(7)

(Part b).

When the truck riches a steady-state speed $\ \frac{dv}{dt}=0$. Combining this condition with equation (7) we find expression of the steady-state speed $\ $

$v=\ \sqrt{\frac{F_0}{\rho dW}}$(8)

(Part c).

Let's rearrange the equation (7) to show how a simple integral from an integral table can be used

to find the expression relating $v(t)$ to $v\left(0\right)$, $t$ and any of the parameters listed in (Part a).

Separating $dt$ in the equation (7) and then integrating from some initial time $t_0$ to some final time $t_1$, we obtain an integral equation for the speed of the truck.

$\int^{t_1}_{t_0}{dt=\int^{v(t_1)}_{v(t_0)}{\left(\frac{M}{F_0-\rho dWv^2}\right)dv}}$(9)

Solution:

Step 1. Data

Organize what you know, and what you are looking for.

Given:

$m=3kg$ - the mass of the block,
$M=2kg$ - the mass of the block,
$\varphi ={30}^{{}^\circ }$ - angle of incline,
$\mu =0.1$ - the coefficient of kinetic friction,
$\left|\overrightarrow{g}\right|=9.81\ m/{sec}^2$ - gravitational acceleration,
$m_p=0$ - the mass of the pulley,
$m_r=0$ - the mass of the rope, the rope is inextensible.

Find:

${\overrightarrow{a}}_1$ - the acceleration of block of mass $M$.

Step 2. Diagram

Let's sketch a diagram to help visualize what is going on. Find all forces involved in the given physical process. Draw free-body diagram with all relevant variables, for describing the process (Figure 3).

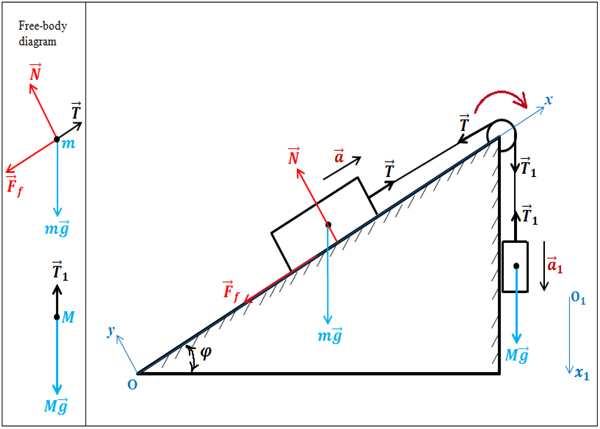
Figure 3.

Reference frame

We will consider the motion of the pulley relative to the Earth - inertial reference frame with the conventional $"xy"$ Cartesian coordinate system. Align axis $"Ox"$ with the direction of the acceleration.

Step 3. Equation

To describe motion of these blocks we are going to use Newton's second law for the case of constant mass (traditional form)

$m\bullet \overrightarrow{a}=\ {\overrightarrow{F}}_{net}$,(1)

where ${\overrightarrow{F}}_{net}=\sum^n_{i=0}{{\overrightarrow{F}}_i}$ - the vector sum of all forces, acting on an object.

Thus, we need to find all forces acting on objects of mass $m$ and mass $M$.

Forces arise as a result of the interaction of objects. Therefore, to identify all forces acting on an object, you first have to answer the question about which objects interact with this object.

Interaction of the block of mass $m$ with:

1. the Earth, gives rise the gravitational force $m\overrightarrow{g}$,
2. the rope, gives rise the rope tension force $\overrightarrow{T}$.
3. the surface of incline, gives rise the force of normal reaction $\overrightarrow{N}$,
4. the surface of incline, gives rise the kinetic friction force ${\overrightarrow{F}}_f$,

Substituting the above listed forces into the right side of equation (1) we have

$m\bullet \overrightarrow{a}= \overrightarrow{T}+m\overrightarrow{g}+\overrightarrow{N}+{\overrightarrow{F}}_f$(2)

Similarly, for the block of mass $M$ we have

$M\bullet {\overrightarrow{a}}_1= {\overrightarrow{T}}_1+M\overrightarrow{g}$(3)

This immediately leads to the question of the direction of the friction force acting on the block of mass $m$. Without the answer to this question, you cannot rewrite the vector equations (2) and (3) in the form of scalar components and therefore find the acceleration. If you don't know acceleration you don't know the direction of the motion of the block. The direction of the kinetic force of friction on the block of mass $m$ is such that it will oppose the relative motion of the block along the surface. We have the vicious circle: to find the acceleration we need to know the direction of the force of friction, but to find the direction of the force of friction we need to know the direction of motion.

To break this vicious circle let us assume that the block of mass $m$ will slide up ($a_x>0$) in the absence of the force of friction. It is clear that adding the force of friction later cannot change the direction of motion and only decreases the magnitude of acceleration.

Thus if we find the direction of acceleration of the block of mass $m$ in the absence of friction (${\overrightarrow{F}}_f=0$), we will find the direction of the force of friction.

Decomposing vectors of the equations (2) and (3) into their components along coordinate-axes $xy$ (Figure 3), and taking into account that ${\overrightarrow{F}}_f=0$, we obtain

$\left.\begin{array}{rl} Ox:&ma_x=T-mg\bullet sin\varphi\\ Oy:&ma_y=0=N-mg\bullet cos\varphi\\ O_1x_1:&Ma_1=Mg-T_1 \end{array}\right\}$ (4)

Now we want to use our simplifications:

• a block is considered a single mass point $\Rightarrow $ all forces are applied at the single point (Figure 3. Free-body diagram),
• the rope and pulley are weightless and frictionless $\Rightarrow $ $\left|\overrightarrow{T}\right|=\left|\ {\overrightarrow{T}}_1\right|$ ,
• the rope is inextensible (the displacement values of both blocks are always equal) $\Rightarrow $ $\left|\overrightarrow{a}\right|=\left|{\overrightarrow{a}}_1\right|$ or $a_x=a_1$.

Substituting these simplifications into the system of linier equations (3), we obtain $a_x\left(m+M\right)=Mg-mg\bullet {sin \varphi \ },$

$a_x=\frac{M-m\bullet {sin \varphi \ }}{m+M}\bullet g$(5)

Substituting data from the step 1 into the equation (5), we have $a_x=0.1\bullet g=0.981\ m/{sec}^2$.

Thus, $a_x>0$ and our assumption that the block of mass $m$ moves along axis $Ox$ in the positive direction was correct. Therefore, the kinetic force of friction is directed in the opposite direction as shown on Figure 3.

Now we can add the force of friction into our consideration with the right sign "$-$" and the system of equations(2) and (3) takes the form $\left.\begin{array}{rl} Ox: &ma_x=T-mg\bullet sin\varphi -F_f\\ Oy: &ma_y=0=N-mg\bullet cos\varphi\\ O_1x_1: &Ma_1=Mg-T_1\\ &F_f=\mu \bullet N \end{array}\right\}$(6)

Solving the above system of liner equations we obtain the required acceleration

$a_1=\frac{M-m\left(sin\varphi +\mu cos\varphi \right)}{m+M}\bullet g$(7)

Answer: $a_1\approx 0.05g\approx 0.49\ m/{sec}^2$

Solution:

Step 1. Data

Organize what you know, and what you are looking for.

Given:

$m\ $- the mass of the ball,
$M$ - the mass of the foot,
$M\gg m$
$v_0$ - the speed of soccer foot

Find:

$v$ - the speed of the soccer ball.

Step 2. Diagram

Let's sketch a diagram to help visualize what is going on. It is very helpful to draw two diagrams, which represent changes of object's position in some time interval $\Delta t$ (Figure 4 a, b), and two diagrams, which represent changes of object's velocities in other reference frame (Figure 4 c, d).

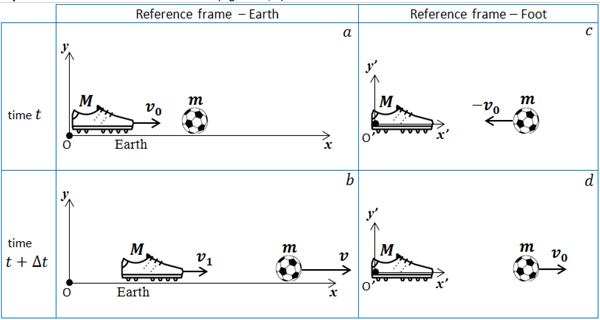
Figure 4.

Reference frame

Let us first consider the motion of the ball relative to the foot - inertial reference frame "x'O'y'". Then we will consider the motions of the foot and the ball relative to the Earth - inertial reference frame "xOy" . Align axis "Ox" with the direction of the motion.

Step 3. Equation

Let's start to solve the problem by using our simplifications:

• the encounter of the foot and the ball will be considered a perfectly elastic central collision, therefore the total kinetic energy of these two bodies after the encounter is equal to their total kinetic energy before the encounter;
• the mass of the foot is much greater than the mass of the ball, therefore the speed of the foot is not changed after the encounter $\ v_1=\ v_0$.

An elastic collision of heavy and light bodies is more convenient to consider in the frame of reference "x'O'y'" , associated with the heavy body - foot (see Figure 4 c, d).

In this reference frame the ball hits the foot at the speed $-v_0$ (Figure 4 c) and bounces off of the foot, like off of the wall, at the speed $v_0$ (Figure 4 d). The value of the speed is not changed after impact, otherwise the kinetic energy would be changed. However, the direction of the ball motion changes to opposite.

The reference frame"x'O'y'", associated with the foot, moves at the speed $\ v_0$ (Figure 4 a) relative to the reference frame "xOy", associated with the Earth. According to the law of addition of velocities (Galilean transformation for velocity) in the transition from one inertial reference frame "x'O'y'" to another inertial reference frame "xOy", we obtain the speed of the ball after the kick relative to the Earth (Figure 4 b)

$v=v_0+v_0=2\bullet v_0 $(1)

$\cdots $

You can solve this problem using the laws of conservation of energy and momentum

$\left.\begin{array}{rl} \text{time } t:&K_1=\frac{m\bullet 0^2}{2}+\frac{M\bullet {{(v}_0)}^2}{2}; P_1=m\bullet 0+M\bullet v_0\\ \text{time } t+\Delta t:&K_2=\frac{m\bullet v^2}{2}+\frac{M\bullet {{(v}_1)}^2}{2}; P_2=-m\bullet v-M\bullet v_1 \end{array}\right.$

The law of conservation of energy $K_1=K_2:$

$\frac{M\bullet {{(v}_0)}^2}{2}=\frac{m\bullet v^2}{2}+\frac{M\bullet {{(v}_1)}^2}{2}$(2)

The law of conservation of momentum $P_1=P_2:$

$M\bullet v_0=-m\bullet v-M\bullet v_1$(3)

Solving the equation (3) for $v_1$

$v_1=\frac{M\bullet v_0-m\bullet v}{M}$

and substituting it in the equation (2) we have

$M\bullet {\left(v_0\right)}^2=m\bullet v^2+M\bullet {\left(v_0-\frac{m}{M}v\right)}^2$

$M\bullet {\left(v_0\right)}^2=m\bullet v^2+M\bullet {{(v}_0)}^2-2\bullet m\bullet v_0\bullet v+\frac{m^2}{M}\bullet v^2$

After some simplifications, we obtain the quadratic equation for $v$

$\left(m+\frac{m^2}{M}\right)\bullet v^2-\left(2\bullet m\bullet v_0\right)\bullet v=0$

This equation has two solutions

$v=0$ (does not make sense)

and

$v=\frac{2}{(1+{m}/{M})}\bullet v_0$

If $M\gg m$, then ${m}/{M}\to 0$ and $v\to 2\bullet v_0$

Thus, we got the same solution (see formula (1)), but in a more complicated way.