Services

A rocket with initial mass m₀ is taking off vertically from a launch pad. Neglecting gravity and drag forces:

• establish the equation of the rocket’s motion with continuous expulsion of the mass of the gas from the rocket nozzle,
• solve this equation.

---

SOLUTION

Step 1. Data

Organize what you know, and what you are looking for.

Given: m0 – the total initial mass of the rocket (including propellant) at the initial time t = 0 $\overrightarrow{u}$ – the velocity of the expelled mass of the gas relative to the rocket, $\overrightarrow{|u}|=u=const$ $\overrightarrow{v}=0$ – the velocity of the rocket at the initial time t = 0 ${\overrightarrow{F}}_g\sim 0$ – gravitational forces, ${\overrightarrow{F}}_d\sim 0$ – the drag force

Find: $v=f(t,u,m,\ m_0)$ – the instantaneous speed of the rocket

Step 2. Diagram

Let us sketch a diagram to help visualize what is going on. Find all forces involved in the given physical process. Draw a free-body diagram with all relevant variables, for describing the process (Figure 1).

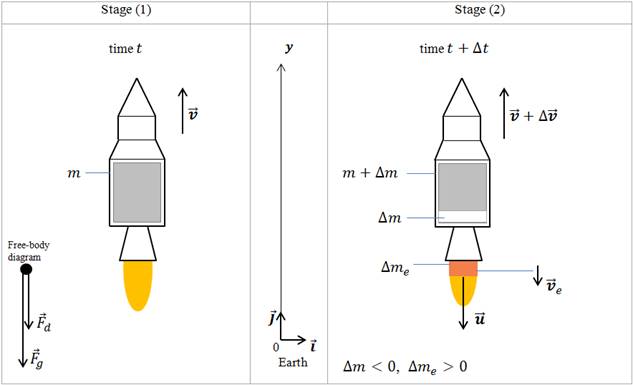
Figure 1.

Reference frame

Let us consider the motion of the rocket relative to the Earth - inertial reference frame $\overrightarrow{i}\ 0\ \overrightarrow{j}$.

Notation

$\overrightarrow{i},\ \overrightarrow{j}$ – basis vectors.

t – the time

$\Delta t$ – the change in time

m₀ – the total initial mass of the rocket (including propellant) at the initial time t=0

m – the total mass of the rocket (including propellant) at time t

$\overrightarrow{v}$ – the instantaneous velocity of the rocket at time t

$\Delta m$ – the change of the mass of the rocket in the time interval $\Delta t$

${\Delta m}_e$ – the change of the expelled mass of the gas in the time interval $\Delta t$

$\Delta \overrightarrow{v}$ – the change of the rocket’s velocity in the time interval $\Delta t$

${\overrightarrow{v}}_e$ – the velocity of the expelled mass of the gas relative to the Earth,

$\overrightarrow{u}$  – the velocity of the expelled mass of the gas relative to the rocket.

Step 3. Equation

The system, consisting of the rocket and expelled mass of gas, is a closed system if there are no external forces acting on it. In this case, however, there are two external forces; gravity and drag forces:

${\overrightarrow{F}}_{net}=\sum^n_{i=0}{{\overrightarrow{F}}_i}$ – the vector sum of gravitational and drag forces.

By the general form of Newton’s second law $\frac{d\overrightarrow{P}}{dt}={\overrightarrow{F}}_{net}$, this equation can be rearranged to read:

$d\overrightarrow{P}={\overrightarrow{F}}_{net}\bullet dt$(1)

where $\overrightarrow{P}$ is the total momentum of the closed system.

Let us consider the system change in a short time interval $\Delta t$, when the rocket expels a small amount of gas $\Delta m$ and obtains a small gain in velocity $\Delta \overrightarrow{v}$. Then the change in momentum of the entire system is expressed by the formula

$\overrightarrow{P}\left(t+\Delta t\right)-\overrightarrow{P}(t)={\overrightarrow{F}}_{net}\bullet \Delta t$(2)

$\overrightarrow{P}(t)=m\overrightarrow{v}$ – the momentum of the system at time t,

$\overrightarrow{P}\left(t+\Delta t\right)=\left(m+\Delta m\right)\left(\overrightarrow{v}+\Delta \overrightarrow{v}\right)+\Delta m_e{\overrightarrow{v}}_e$ – the momentum of the system at time $\left(t+\Delta t\right)$.

We note here that despite the + sign in front of $\Delta m$, the rocket mass decreases, so $\Delta m<0$.

Substituting the above expressions into equation (2), we have

$\left(m+\Delta m\right)\left(\overrightarrow{v}+\Delta \overrightarrow{v}\right)+\Delta m_e{\overrightarrow{v}}_e-m\overrightarrow{v}={\overrightarrow{F}}_{net}\bullet \Delta t$(3)

The law of conservation of mass, $\Delta m_e+\Delta m=0$ entails

$\Delta m_e=-\Delta m$(4)

Finally, the velocity of the expelled mass of gas relative to the Earth at the time $\left(t+\Delta t\right)$ can be expressed as the sum of velocities

${\overrightarrow{v}}_e=(\overrightarrow{v}+\Delta \overrightarrow{v})+\overrightarrow{u}$(5)

Decomposing these vectors onto basis vectors of the selected reference frame (Figure 1), we obtain $(\overrightarrow{v}+\Delta \overrightarrow{v})=(v+\Delta v)$ $\bullet \overrightarrow{j}$ and $\overrightarrow{u}=-\ u\bullet $ $\overrightarrow{j}$, where v and u are the magnitudes of $\overrightarrow{v}$ and $\overrightarrow{u}$ respectively.

The direction (sign) of the velocity ${\overrightarrow{v}}_e$ has been defined by the ratio of speeds: $(v+\Delta v)>u$ or $(v+\Delta v) < u$ .

The magnitude u is a substantially positive value (for rockets using chemical propellant, u = 4 km/sec).Thus, in the beginning of the flight, v < u, but after several minutes of flight, v > u.

Substituting equations (4) and (5) into the momentum equation (3), we obtain

$\left[\left(m+\Delta m\right)\left(\overrightarrow{v}+\Delta \overrightarrow{v}\right)-\Delta m\left(\overrightarrow{v}+\Delta \overrightarrow{v}+\overrightarrow{u}\right)\right]-\left[m\overrightarrow{v}\right]={\overrightarrow{F}}_{net}\bullet \Delta t$

$\left[m\overrightarrow{v}+m\Delta \overrightarrow{v}+\Delta m\overrightarrow{v}+\Delta m\Delta \overrightarrow{v}-\Delta m\overrightarrow{v}-\Delta m\Delta \overrightarrow{v}-\Delta m\overrightarrow{u}\right]-\left[m\overrightarrow{v}\right]={\overrightarrow{F}}_{net}\bullet \Delta t$

We now see that several terms in the equation cancel each other out (canceling pairs are marked in the same color), and the equation takes the simpler form:

$m\Delta \overrightarrow{v}-\Delta m\overrightarrow{u}={\overrightarrow{F}}_{net}\bullet \Delta t$(6)

This is the equation of the rocket’s motion with a variable mass under the action of external forces for a finite time interval $\Delta t$.

Let us assume that the change in the mass of the rocket occurs continuously, without jumps, so that there exists a derivative dm/dt.

Divide both parts of equation (6) by $\Delta t$ and rewrite it in the form of limit, when $\Delta t\to 0$.

${\mathop{lim}_{\Delta t\to 0} (m\frac{\Delta \overrightarrow{v}}{\mathit{\Delta}t}\ )\ }={\overrightarrow{F}}_{net}+{\overrightarrow{u}\mathop{lim}_{\Delta t\to 0} (\frac{\mathit{\Delta}m}{\mathit{\Delta}t}\ )\ }$

$m\frac{d\overrightarrow{v}}{dt}={\overrightarrow{F}}_{net}+\overrightarrow{u}\frac{dm}{dt}$(7)

We have thus established the equation of the rocket’s motion with continuous expulsion of the mass of the gas from the rocket nozzle and with the presence of a net external force. Keep in mind that dm/dt < 0.

-------

Let us apply this equation to solve the problem of rocket motion without external forces.

Assuming ${\overrightarrow{F}}_{net}=0,$ (conservation of momentum) the equation (7) takes the form

$m\frac{d\overrightarrow{v}}{dt}=\overrightarrow{u}\frac{dm}{dt}$(8)

Since the direction of the rocket motion is parallel to the vector $\overrightarrow{j}$ , we can write $\frac{d\overrightarrow{v}}{dt}=\frac{dv}{dt}\overrightarrow{j}$, (as $\frac{d\overrightarrow{j}}{dt}=0$).

We can now rewrite equation (8) in the form of a projection onto the basis vector $\overrightarrow{j}$

$m\frac{dv}{dt}\overrightarrow{j}=-\ u\frac{dm}{dt}\overrightarrow{j}.$

Finally, the above equation can be written in scalar form as

$m\frac{dv}{dt}=-\ u\frac{dm}{dt}$(9)

The speed u of the expelled mass of gas relative to the rocket is substantially positive and constant in our case.

Simplifying and integrating the equation (9), we have

$v=-u\bullet \int{\frac{dm}{m}}=-u\bullet ln\ m+C.$

The value of the constant C has been defined from initial conditions:

v = 0 – the speed of the rocket at the initial time t = 0,

m₀ – the total initial mass of the rocket (including propellant) at the initial time t = 0.

Thus, the above equation gives: $0=-u\bullet ln\ m_0+C,$ or $\ \textrm{С}=u\bullet ln\ m_0.$

This finally gives us the solution of equation (9), which is called Tsiolkovsky’s equation:

$v=u\bullet ln\frac{m_0}{m}$(10)

A rocket with initial mass m₀ is taking off vertically from a launch pad. Neglecting gravity and drag forces:

1) establish the equation of the rocket’s motion when gas is ejected in small, discrete portions from the rocket nozzle,

2) determine in which case the velocity of the rocket will be higher – in the case of continuous ejection of mass of gas {see Problem 1} or discrete ejection of small portions of the same mass of gas $\Delta m$?

Step 1. Data

Organize what you know, and what you are looking for.

Given: m0 – the total initial mass of the rocket (including propellant) at the initial time t=0 $\overrightarrow{u}$ – the velocity of the expelled mass of gas relative to the rocket, $\overrightarrow{|u}|=u=const$, $\overrightarrow{v}=0$– the velocity of the rocket at the initial time t = 0 ${\overrightarrow{F}}_g\sim 0$ – gravitational forces, ${\overrightarrow{F}}_d\sim 0$ – the drag force

Find: 1) $v_{nd}=f(n,u,\ m_0)$– the instantaneous speedof the rocket after discrete ejection of the n th portion of gas, 2) speeds relation $v_n/v_{nd}$ with each next gas ejection.

Step 2. Diagram

Let us sketch a diagram to help visualize what is going on. Find all forces involved in the given physical process. Draw a free-body diagram with all relevant variables, for describing the process (Figure 2).

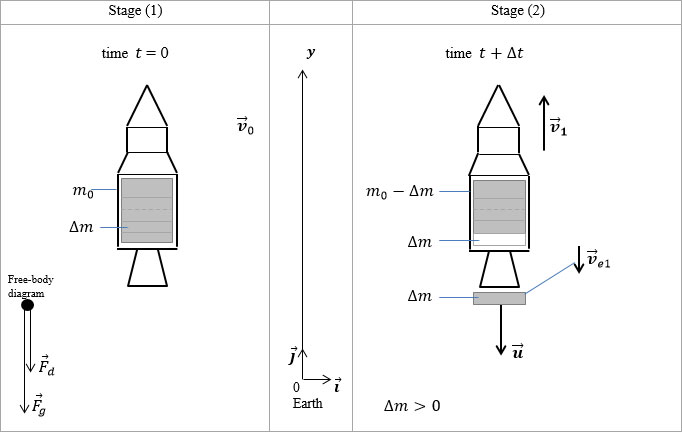
Figure 2.

Reference frame

Let us consider the motion of the rocket relative to the Earth - inertial reference frame $\overrightarrow{i}\ 0\ \overrightarrow{j}$.

Notation

${\overrightarrow{v}}_n$ – the instantaneous velocity of the rocket after continuous ejection of mass of gas equals to n portions of gas,

${\overrightarrow{v}}_{nd}$ – the instantaneous velocity of the rocket after discrete ejection of the n th portion of gas,

Step 3. Equation

1) Let us consider an imaginary case, when the rocket ejects gas not continuously but in small discrete portions of equal mass of gas $\Delta m$ (Figure 2). Assume that this portion of mass $\Delta m$ gets the same velocity $\overrightarrow{u}$, relative to the rocket, in each gas ejection. The direction of the velocity $\overrightarrow{u}$ is opposite to the direction of the basis vector $\overrightarrow{j}$. Determine the velocity ${\overrightarrow{v}}_N$ that the rocket will reach after N gas ejections, if the initial mass of the rocket was equal to m₀ and the initial velocity ${\overrightarrow{v}}_0$ was equal to zero.

${\overrightarrow{v}}_1$, ${\overrightarrow{v}}_2$,  … – velocities of the rocket after 1st, 2nd,… gas ejections relative to the Earth - inertial reference frame $\overrightarrow{i}\ 0\ \overrightarrow{j}$

By the law of conservation of momentum

$\left(m_0-\Delta m\right){\overrightarrow{v}}_1+\Delta m{\overrightarrow{v}}_{e1}=0$, where we took into account that in this case $\Delta m>0$ and ${\overrightarrow{v}}_{e1}$ – the velocity of ejected mass of gas after the first ejection relative to the Earth.

Using the expression for vector sum of velocities ${\overrightarrow{v}}_{e1}={\overrightarrow{v}}_1+\overrightarrow{u}$ , we have

$m_0{\overrightarrow{v}}_1-\Delta m{\overrightarrow{v}}_1+\Delta m{\overrightarrow{v}}_1+\Delta m\overrightarrow{u}=0$,

$m_0{\overrightarrow{v}}_1+\Delta m\overrightarrow{u}=0$.

Rewriting the above equation in the form of projections of vectors onto basis vector $\overrightarrow{j}$, we get

$m_0v_1\overrightarrow{j}-\Delta mu\overrightarrow{j}=0$.

In scalar form, the expression for the speed of the rocket, after the first ejection, takes on the form $v_1=\frac{\Delta m}{m_0}u$(1)

where v₁ and u are the magnitudes of ${\overrightarrow{v}}_1$ and $\overrightarrow{u}$ respectively.

We now find v₂. In the frame of reference moving with the speed v₁, the rocket is stationary before the second ejection of mass, and it acquires the velocity v₂ - v₁ after the second ejection. Therefore, we can use formula (1), making the substitution $m_0\to \ m_0-\Delta m$, $v_2\to \ v_2-v_1$. Thus, we have

$v_2{-v}_1=\frac{\Delta m}{m_0-\Delta m}u$.

Combining this relation with (1), we find v₂

$v_2=\left[\frac{\Delta m}{m_0}+\frac{\Delta m}{m_0-\Delta m}\right]\bullet u$.

Continuing this process further, it is not difficult to obtain an expression for the speed v_N that the rocket will acquire after N gas ejections

$v_N=\left[\frac{\Delta m}{m_0}+\frac{\Delta m}{m_0-\Delta m}+\dots +\frac{\Delta m}{m_0-\left(N-1\right)\Delta m}\right]\bullet u\, where N\in \{1,\ 2,\ 3\dots \}$(2)

Let us divide the entire mass of the rocket m₀ into 100 equal parts, and let $\Delta m=\frac{m_0}{100}$.

Using the equation (2) we shall obtain

$v_{1d}=[{{\frac{1}{100}}}\ ]\bullet u$ – the speed of the rocket after the ejection of the 1st portion of gas (d – discrete),

$v_{2d}=[{{\frac{1}{100}}}+{{\frac{1}{99}}}\ ]\bullet u$ – the speed of the rocket after the ejection of the 2nd portion of gas.

Finally, the speed of the rocket after the ejection of the Nth portion of gas is

$v_{Nd}=[{{\frac{1}{100}}}+{{\frac{1}{99}}}\ +\dots +{{\frac{1}{100-(N-1)}}}]\bullet u, where N\in \{1,2,\dots ,100\}$(3)

2) To answer the second question we shall consider the case when a rocket ejects 50% of its mass (93% of total mass of a real rocket is propellant). We want to compare the value of speeds v_n  and v_nd when n = 50.

A) Discrete ejection of exhaust gases

Let us introduce the following notation for the Nth partial sum of the harmonic series

$H_N=\ \sum^N_{i=1}{({{\frac{1}{i}}}})=[1+{{\frac{1}{2}}}\ +{{\frac{1}{3}}}+\dots +{{\frac{1}{N}}}]$, then $H_N-H_{N-n}=\ \sum^N_{i=1}{({{\frac{1}{i}}}})-\sum^{N-n}_{i=1}{({{\frac{1}{i}}}})= \sum^{N-n}_{i=1}{({{\frac{1}{i}}}})+\sum^N_{i=N-n+1}{({{\frac{1}{i}}}})-\sum^{N-n}_{i=1}{({{\frac{1}{i}}}})=\sum^N_{i=N-n+1}{({{\frac{1}{i}}}})$(4)

Thus, expression (3) for the rocket’s speed with the ejection of small discrete portions of equal mass of the gas are written as

$v_{1d}=[H_{100}-H_{99}\ ]\bullet u, v_{2d}=[H_{100}-H_{98}]\bullet u, v_{3d}=[H_{100}-H_{97}]\bullet u and v_{nd}=\left[H_{100}-H_{100-n}\ \right]\bullet u, where n\in \{1,2,\dots ,50\}$(5)

Combining (4) и (5) we shall obtain

$v_{nd}=u\bullet \sum^{100}_{i=100-n+1}{({{\frac{1}{i}}}})$, where $n\in \{1,2,\dots ,50\}$(6)

B) Continuous ejection of exhaust gases

In case of continuous ejection of the mass of the gas, the rocket’s speed is given by (from Problem #1)

$v=u\bullet ln\frac{m_0}{m}\$(7)

Using the fact that we divided the initial mass of the rocket m₀ into 100 equal parts, we set $\Delta m=\frac{m_0}{100}$, and find values for rocket speeds after continuous outflow of identical masses of gas:

$v_1=u\bullet ln\frac{m_0}{m_1}=u\bullet ln{{\frac{100}{99}}}$ – the speed of the rocket after outflow of the mass of the gas $\Delta m$,

the mass of the rocket has become $m_1=m_0-\Delta m=m_0\bullet {{\frac{99}{100}}}$ .

$v_2=u\bullet ln\frac{m_0}{m_2}=u\bullet ln{{\frac{100}{98}}}$ – the speed of the rocket after outflow of the mass of gas $2\bullet \Delta m$,

the mass of the rocket has become $m_2=m_0-2\bullet \Delta m=m_0\bullet {{\frac{98}{100}}}$ .

$v_n=u\bullet ln\frac{m_0}{m_n}=u\bullet ln{{\frac{100}{100-n}}}$ – the speed of the rocket after outflow of the mass of gas $n\bullet \Delta m$(8)

the mass of the rocket has become$\ m_n=m_0-n\bullet \Delta m=m_0\bullet {{\frac{(100-n)}{100}}}$ .

In our case the rocket ejects 50% of its mass, that means n = 50 and the above expression can be rewritten as

$m_{50}=m_0-50\bullet \Delta m=m_0\bullet {{\frac{50}{100}}}$

To answer the second question – in what gas outflow, discrete or continuous, does the rocket acquire higher speed – graph the relation of two speeds (6) and (8).

${{\frac{v_n}{v_{nd}}}}={{\frac{u\bullet ln\left({{\frac{100}{100-n}}}\right)}{u\bullet \left[\sum^{100}_{i=100-n+1}{{{\left(\frac{1}{i}\right)}}}\right]}}}=\frac{ln\left({{\frac{100}{100-n}}}\right)}{\left[\sum^{100}_{i=100-n+1}{{{\left(\frac{1}{i}\right)}}}\right]}$(9)

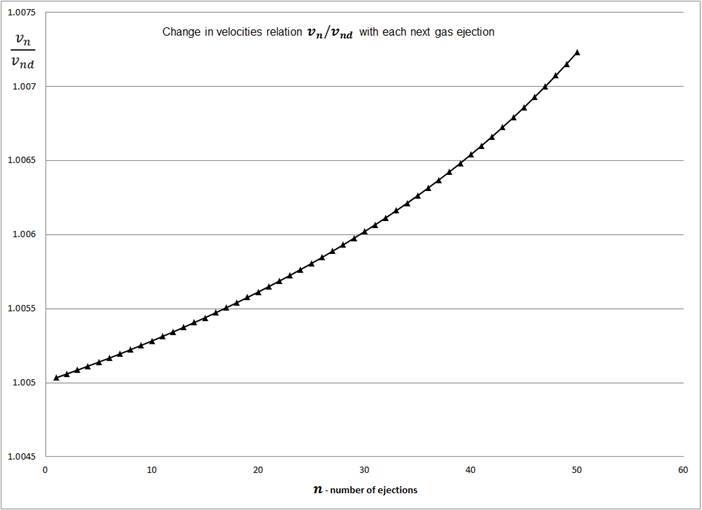
Figure 2.

Figure 2 shows the increase in speeds relation $v_n/v_{nd}$ as the amount of ejected gas increases.

This points to the fact that the rocket’s speed increases faster in the case of continuous ejection of the mass of the gas, than in case of discrete ejection of the same mass of the gas.