Services

Solution:

First we are going to solve the homogenous equation: y'''' + 2y''' + y'' = 0

Let’s think about what we know about this equation:

1. This is a fourth-order linear differential equation.
2. If k is a distinct real root, then y = e^kt is a solution.
3. If k is a real root and appears r times then y = e^kt, y = te^kt, y = t²e^kt, …, y = t^k-1e^-kt are all solutions.
4. We know that the general solution is of the form: y₀ = C₁ + C₂t + C₃e^kt + C₄e^ktt, where C₁, C₂, C₃, C₄ are all constants.

First we will write the characteristic polynomial:

k⁴ + 2k³ + k² = 0
k²(k² + 2k + 1) = 0

To determine the solution to this equation, either k² or (k² + 2K + 1) must equal zero.

k² = 0 yields k₁ = 0 and k₂ = 0. (We should expect two solutions since the equation is second order. We can then solve k² + 2K + 1 = 0 using the quadratic function. This yields: k₃ = -1 and k₄ = -1.

Thus using facts 2-4 written above, we can plug in for our four k constants into y₀ = C₁ + C₂t + C₃e^kt + C₄e^ktt:

     k₁ = 0: C₁

     k₂ = 0: C₂t

     k₃ = -1: C₃e^-t

     k₄ = -1: C₄e^-tt

Thus the net homogenous solution is: y₀ = C₁ + C₂t + C₃e^-t + C₄e^-tt.

Now we can proceed and solve for the nonhomogeneous equation g(t) = x² + x - 1.

We let Y be a generic fourth order polynomial matching our original equation:

Y = Ax⁴ + Bx³ + Cx²

g(t)' = 4At³ + 3Bt² + 2C

g(t)'' = 12At² + 6Bt + 2C

g(t)''' = 24At + 6B

g(t)'''' = 24A

We plug each derivative of g(t) to the corresponding derivate of y in the original left hand side of the fourth-order linear equation:

24A + 2(24Ax + 6B) + 12Ax² + 6Bx + 2C = x² + x - 1

Now we can combine like terms and simplify the left hand side:

12Ax² + (48A + 6B)x + (2C + 24A + 12B) = x² + x - 1

We can then setup the system of linear equations by equating the coefficients of equal powers:

$$\left.\begin{matrix} x^{2} : 12A = 1\\ x : 48A + 6B = 1\\ 1: 2C + 24A + 12B = -1\\ \end{matrix}\right.\rightarrow \left.\begin{matrix} A = \frac{1}{12}\\ B = -\frac{1}{2}\\ C = \frac{3}{2}\\ \end{matrix}\right.\rightarrow Y = \frac{x^{4}}{12} - \frac{x^{3}}{2} + \frac{3}{2}x^{2}$$

The complete solution is the sum of the homogenous and nonhomogeneous solutions:

y = y₀ + g(t)

$$y = C_{1} + C_{2}t + C_{3}e^{-t} + C_{4}e^{-t}t + \frac{t^{4}}{12} - \frac{t^{3}}{2} + \frac{{3}}{2}t^{2}$$

Solution:

First we are going to solve the homogenous equation: y''- 4y''+ 4y' = 0

Let's think about what we know about this equation:

1. This is a second-order linear differential equation.
2. If k is a distinct real root, then y=e^kt is a solution.
3. If k is a real root and appears r times then y=e^kt, y=te^kt, y=t²e^kt, ..., y=t^k-1e^-kt are all solutions.
4. We know that the general solution is of the form: y₀=C₁+C₂e^kt+C₃e^kt, where C₁, C₂, C₃ are all constants.

First we will write the characteristic polynomial:

k³ - 4k² + 4k² = 0
k(k² - 4k + 4) = 0

To determine the solution to this equation, either k or  (k² - 4k + 4) must equal zero.

k=0 yields k₁=0. We can then solve k² - 4k + 4=0 using the quadratic function. This yields: k₂=2 and k₃=2.

Thus using facts 2-4 written above, we can plug in for our four k constants into y₀=C₁+C₂e^kt+C₃e^ktt:

     k₁ = 0: C₁

     k₂ = 2: C₂e^kt

     k₃ = 2: C₃e^ktt

Thus the net homogenous solution is: y₀ = C₁ + C₂e^2t + C₃e^2tt.

Now we can proceed and solve for the nonhomogeneous equation g(t) = (t - 1)e^t.

We let Y be a generic second order polynomial matching our original equation:

Y=(Ax+B)e^x

g(t)' = Ae^t + (At + B)e^t

g(t)'' = Ae^t + Ae^t + (At + B)e^t = 2Ae^t + (At + B)e^t

g(t)''' = 2Ae^t + Ae^t + (At + B)e^t = 3Ae^t + (At + B)e^t

We plug each derivative of g(t) to the corresponding derivate of y in the original left hand side of the second-order linear equation:

3Ae^x + (Ax + B)e^x - 4(2Ae^x + (Ax + B)e^x) + 4(Ae^x + (Ax + B)e^x) = (x - 1)e^x

Now we can combine like terms and simplify the left hand side:

-Ae^x + (Ax + B)e^x = (x - 1)e^x

We can then setup the system of linear equations by equating the coefficients of equal powers:

 $$\left.\begin{matrix} e^{x} : -A + B = -1\\ xe^{x}: A = 1\\ \end{matrix}\right.\rightarrow \left.\begin{matrix} B = 0\\ A = 1\\ \end{matrix}\right.\rightarrow Y = xe^{x}$$

The complete solution is the sum of the homogenous and nonhomogeneous solutions:

y = y₀ + g(t)

y = C₁ + C₂e^2t + C3e^2tt + te^t

Solution:

First we are going to solve the homogenous equation: y'' - 2y' = 0

Let's think about what we know about this equation:

1. This is a second-order linear differential equation.
2. If k is a distinct real root, then y = e^kt is a solution.
3. If k is a real root and appears r times then y = e^kt, y = te^kt, y = t²e^kt, ..., y = t^k-1e^-kt are all solutions.
4. We know that the general solution is of the form: y₀ = C₁ + C₂e^kt, where C₁, C₂ are all constants.

First we will write the characteristic polynomial:

k² + 2k = 0

k(k + 2) = 0

To determine the solution to this equation, either k or (k+2) must equal zero.

k=0 yields k₁=0. We can then solve k + 2 = 0 using the quadratic function. This yields: k₂ = -2.

Thus using facts 2-4 written above, we can plug in for our four k constants into y₀ = C₁ + C₂e^kt:

k₁ = 0: C₁

k₂ = -2: C₂e^-2t

Thus the net homogenous solution is: y₀ = C₁ + C₂e^-2t:

 Now we can proceed and solve for the nonhomogeneous equation g(t) = e^t (sin⁡ t+cos ⁡t).

 We let Y be a generic second order polynomial matching our original equation: Y = e^x(A sin x + B cos ⁡x)

g(t)' = e^t(A sin t + B cos⁡t) + e^t(A sin t - B cos t)

g(t)''= e^t(A sin t + B cos t) + e^t(A sin t - B cos t)+ e^t(A sin t - B cos t) + e^t(-A sin t - B cos ⁡t)

We plug each derivative of g(t) to the corresponding derivate of y in the original left hand side of the second-order linear equation:

e^x(A sin x + B cos ⁡x) + e^x(A sin x - B cos x) + e^x(A sin x - B cos⁡ x) + e^x(A sin x - B cos⁡ x) + 2(e^x(A sin x + B cos ⁡x) + e^x(-A sin x - B cos ⁡x)) = e^x(sin x + cos ⁡x)

Now we can combine like terms and simplify the left hand side:

3e^x(A sin x + B cos ⁡x) +3(A sin x - B cos x) + 2e^x(-A sin x - B cos ⁡x) = e^x(sin x + cos ⁡x)

We can then setup the system of linear equations by equating the coefficients of equal powers:

 $$\left.\begin{matrix} -4B + 2A = 1\\ 4A + 2B = 1\\ \end{matrix}\right.\rightarrow \left.\begin{matrix} A = \frac{3}{10}\\ B = -\frac{1}{10}\\ \end{matrix}\right.\rightarrow Y = e^t(\frac{3}{10}sin x + -\frac{1}{10}cos x)$$

The complete solution is the sum of the homogenous and nonhomogeneous solutions: \[{y=\ y}_0\ +g\left(t\right)\] \[y\ =\ C_1+\ C_2e^{-2t}+e^t(\frac{3}{10}{sin t\ }+\ -\frac{1}{10}{cos t)\ }\]

Solution:

First we are going to solve the homogenous equation: y'' - 4y' = 0

Let's think about what we know about this equation:

1. This is a second-order linear differential equation.
2. If k is a distinct real root, then y = e^kt is a solution.
3. If k is a real root and appears r times then y = e^kt, y = te^kt, y = t²e^kt, ..., y = t^k-1e^-kt are all solutions.
4. We know that the general solution is of the form: y₀ = C₁ + C₂e^kt, where C₁, C₂ are all constants.

First we will write the characteristic polynomial:

k² - 4k = 0

k(k - 4) = 0

To determine the solution to this equation, either k or (k-4) must equal zero.

k = 0 yields k₁ = 0. We can then solve k - 4 = 0 using the quadratic function. This yields: k₂ = 4.

Thus using facts 2-4 written above, we can plug in for our four k constants into y₀ = C₁ + C₂e^kt:

    k₁ = 0: C₁

    k₂ = 4: C₂e^4t

Thus the net homogenous solution is: y₀ = C₁ + C₂e^4t.

 Now we can proceed and solve for the nonhomogeneous equation g(t) = 16 cosh 4t.

 We let Y be a generic second order polynomial matching our original equation: Y =  C₁(t) + C₂e^4t.

We can now create a system of equations:

C₁(t) + C₂(t)e^4t = 0

C₁(t)*0 + 4C₂(t)e^4t = 16 cosh 4t

Now we can solve the system of equations:

\[\mathit{\Delta}\ =\ \left| \begin{array}{cc} 1 & e^{4t} \\ 0 & 4e^{4t} \end{array} \right| = 4e^{4t}\]

\[{\mathit{\Delta}}_1\ =\ \left| \begin{array}{cc} 0 & e^{4t} \\ 16\ {cosh 4t\ } & 4e^{4t} \end{array} \right| = -16\ {e^{4t}cosh 4t\ }\] \[{\mathit{\Delta}}_2\ =\ \left| \begin{array}{cc} 1 & 0 \\ 0 & 16\ {cosh 4t\ } \end{array} \right| = 16\ {cosh 4t\ }\]

We take the derivate of C₁ and C₂ and then integrate:

\[C_1'=\ \frac{{\mathit{\Delta}}_1}{\mathit{\Delta}}=\ \frac{-16\ {e^{4t}cosh 4t\ }}{4e^{4t}}= -4{cosh 4t\ }\] \[C_1\left(t\right)=\ \int{-4{cosh 4t\ }\ dt}=\ -\int{{cosh 4t\ }\ d(4t})=-{sinh 4t+e_1\ }\] \[C_2'=\ \frac{{\mathit{\Delta}}_2}{\mathit{\Delta}}=\ \frac{16\ {cosh 4t\ }}{4e^{4t}}\ = \frac{4{cosh 4t\ }}{e^{4t}}\ = \frac{4}{e^{4t}} * \frac{e^{4t}+\ e^{-4t}}{2} = 2 (1 + e^{-8t}\ )\] \[C_2\left(t\right)=\ 2\int{\left(1\ +\ e^{-8t}\right)dt}=\ 2t-\ \frac{1}{4}e^{-8t}\ +\ C_2\ \]

Now we substitute in C₁(t) and C₂(t):

$$Y=\ {-sinh 4t\ }+\ C_1+ (2t-\ \frac{1}{4}e^{-8t}\ +\ C_2)\ e^{4t},$$ where C₁ = C₂ = 0

The complete solution is the sum of the homogenous and nonhomogeneous solutions:

\[{y=\ y}_0\ +Y\] \[y\ =\ C_1+\ C_2e^{4t}\ {-sinh 4t\ }+(2te^{4t}-\ \frac{1}{4}e^{-8t})\]

Solution.

Let's first find the first-derivative. \[\begin{array}{l} {f'_{x} (x,y)=y-2x\cos y^{2} } \\ {f'_{x} (3,1)=1-2\cdot 3\cos 1=1-6\cos 1\approx -2.24} \end{array}\] \[f'_{y} (x,y)=x-x^{2} \cdot (-\sin y^{2} )\cdot 2y=x+2yx^{2} \sin y^{2} \] \[f'_{y} (3,1)=3+2\cdot 9\cdot \sin 1\approx 18.15\] Let's find the the cosine directional of the vector $$\bar{a}=(2,4)$$ \[\cos \alpha =\frac{2}{\sqrt{2^{2} +4^{2} } } =\frac{2}{\sqrt{20} } =\frac{1}{\sqrt{5} } \approx 0.4472\] \[\cos \beta =\frac{4}{\sqrt{2^{2} +4^{2} } } =\frac{4}{\sqrt{20} } =\frac{2}{\sqrt{5} } \approx 0.8944\] The directional derivative is then: \[\begin{array}{l} {\left. f'_{v} \right|_{A} =f'_{x} (3,1)\cos \alpha +f'_{y} (3,1)\cos \beta =-2.24\cdot 0.4472+18.15\cdot 0.8944\approx -{\rm 1,001728}+{\rm 16,23336}\approx 15.23} \end{array}\]

Solution.

Let's find the coordinates of the points of intersection, then we'll plug in the parametric expressions for each curve in the function of the plane.

\[6t^{2} -(t^{2} )^{2} =1\] \[\begin{array}{l} {t^{4} -6t^{2} +1=0} \\ {t^{2} =\frac{6\pm \sqrt{36-4} }{2} =\frac{6\pm 4\sqrt{2} }{2} =3\pm 2\sqrt{2} } \end{array}\] \[\begin{array}{l} {t_{1} =+\sqrt{3-2\sqrt{2} } =\sqrt{2} -1;} \\ {t_{2} =-\sqrt{3-2\sqrt{2} } =1-\sqrt{2} } \\ {t_{3} =\sqrt{3+2\sqrt{2} } =\sqrt{2} +1} \\ {t_{4} =-\sqrt{3+2\sqrt{2} } =-1-\sqrt{2} } \end{array}\]

We get 4 points of intersection:

\[\begin{array}{l} {M_{1} (\sqrt{2} -1;10\sqrt{2} -14;3-2\sqrt{2} )} \\ {M_{2} (1-\sqrt{2} ;14-10\sqrt{2} ;3-2\sqrt{2} )} \\ {M_{3} (\sqrt{2} +1;14+10\sqrt{2} ;3+2\sqrt{2} )} \\ {M_{4} (-\sqrt{2} -1;-14-10\sqrt{2} ;3+2\sqrt{2} )} \end{array}\]

Now let's find the tangential vector to the curve at these points

\[x'=1;\quad y'=6t^{2} ;\quad z'=2t\] \[\begin{array}{l} {\bar{l}_{1} =(1;18-12\sqrt{2} ;2\sqrt{2} -2)} \\ {\bar{l}_{2} =(1;18-12\sqrt{2} ;2-2\sqrt{2} )} \\ {\bar{l}_{3} =(1;18+12\sqrt{2} ;2\sqrt{2} +2)} \\ {\bar{l}_{4} =(1;18+12\sqrt{2} ;-2-2\sqrt{2} )} \end{array}\]

Let's build the function for the tangential vector to the plane at the determined points

$$\begin{array}{l} {F(x,y,z)=6x^{2} -z^{2} -1=0} \\ {F'_{x} =12x;\quad F'_{y} =0;\quad F'_{z} =-2z} \end{array}$$

At this point

$$M_{1} (\sqrt{2} -1;10\sqrt{2} -14;3-2\sqrt{2} )$$ the tangent to the plane is: $$\begin{array}{l} {(12\sqrt{2} -12)(x-\sqrt{2} +1)+(4\sqrt{2} -6)(z+2\sqrt{2} -3)=0} \\ {(12\sqrt{2} -12)x+(4\sqrt{2} -6)z-2=0} \\ {(6\sqrt{2} -6)x+(2\sqrt{2} -3)z-1=0} \\ {\bar{n}_{1} =(6\sqrt{2} -6;0;2\sqrt{2} -3)} \end{array}$$

At this point

$$M_{2} (1-\sqrt{2} ;14-10\sqrt{2} ;3-2\sqrt{2} )$$ the tangent to the plane is: \[\begin{array}{l} {(12-12\sqrt{2} )(x+\sqrt{2} -1)+(4\sqrt{2} -6)(z+2\sqrt{2} -3)=0} \\ {(6-6\sqrt{2} )x+(2\sqrt{2} -3)z-1=0} \end{array}\] \[\bar{n}_{2} =(6-6\sqrt{2} ;0;2\sqrt{2} -3)\]

At this point

$$M_{3} (\sqrt{2} +1;14+10\sqrt{2} ;3+2\sqrt{2} )$$

the tangent to the plane is:

\[\begin{array}{l} {(12\sqrt{2} +12)(x-\sqrt{2} -1)+(-6-12\sqrt{2} )(z-3-2\sqrt{2} )=0} \\ {(12\sqrt{2} +12)x-(6+12\sqrt{2} )z+30+24\sqrt{2} =0} \\ {(2\sqrt{2} +2)x-(1+2\sqrt{2} )z+5+4\sqrt{2} =0} \end{array}\] \[\bar{n}_{3} =(2\sqrt{2} +2;0;-2\sqrt{2} -1)\]

At this point

$$M_{4} (-\sqrt{2} -1;-14-10\sqrt{2} ;3+2\sqrt{2} )$$

the tangent to the plane is:

\[\begin{array}{l} {-(12\sqrt{2} +12)(x+\sqrt{2} +1)+(-6-12\sqrt{2} )(z-3-2\sqrt{2} )=0} \\ {-(12\sqrt{2} +12)x-(6+12\sqrt{2} )z+30+24\sqrt{2} =0} \\ {-(2\sqrt{2} +2)x-(1+2\sqrt{2} )z+5+4\sqrt{2} =0} \end{array}\] \[\bar{n}_{4} =(-2\sqrt{2} -2;0;-2\sqrt{2} -1)\]

The angle between the curve and the plane is considered to be the angle between the tangent to the line and the tangent to the plane. It can be calculated by the scalar of the vector derivate perpendicular to the plane and the vector tangent to the line.

\[\begin{array}{l} {\bar{l}_{1} =(1;18-12\sqrt{2} ;2\sqrt{2} -2)} \\ {\bar{l}_{2} =(1;18-12\sqrt{2} ;2-2\sqrt{2} )} \\ {\bar{l}_{3} =(1;18+12\sqrt{2} ;2\sqrt{2} +2)} \\ {\bar{l}_{4} =(1;18+12\sqrt{2} ;-2-2\sqrt{2} )} \end{array}\]

\[\begin{array}{l} {\alpha _{1} =\arcsin \frac{\bar{l}_{1} \bar{n}_{1} }{\left|\bar{l}_{1} \right|\left|\bar{n}_{1} \right|} =\arcsin \frac{6\sqrt{2} -6+0+(2\sqrt{2} -2)(2\sqrt{2} -3)}{\sqrt{1+(18-12\sqrt{2} )^{2} +(2\sqrt{2}-2)^{2} } \sqrt{(6\sqrt{2}-6)^{2} +0+(2\sqrt{2} -3)^{2} } } = \arcsin \frac{8-4\sqrt{2} }{\sqrt{625-440\sqrt{2} } \sqrt{125-84\sqrt{2} } } \approx \arcsin (0.4049)\approx 0.42(rad)} \end{array}\]

\[\begin{array}{l} {\alpha _{2} =\arcsin \frac{\bar{l}_{2} \bar{n}_{2} }{\left|\bar{l}_{2} \right|\left|\bar{n}_{2} \right|} =\arcsin \frac{6-6\sqrt{2} +0-(2\sqrt{2} -2)(2\sqrt{2} -3)}{\sqrt{1+(18-12\sqrt{2} )^{2} +(2-2\sqrt{2})^{2} } \sqrt{(6-6\sqrt{2})^{2} +0+(2\sqrt{2} -3)^{2} } } = \arcsin \frac{8-4\sqrt{2} }{\sqrt{625-440\sqrt{2} } \sqrt{125-84\sqrt{2} } } \approx \arcsin (-0.4049)\approx -0.42(rad)} \end{array}\]

\[\begin{array}{l} {\alpha _{3} =\arcsin \frac{\bar{l}_{3} \bar{n}_{3} }{\left|\bar{l}_{3} \right|\left|\bar{n}_{3} \right|} =\arcsin \frac{2\sqrt{2}+2+0-(2\sqrt{2} +1)(2\sqrt{2} +2)}{\sqrt{1+(18+12\sqrt{2} )^{2} +(2+2\sqrt{2})^{2} } \sqrt{(2\sqrt{2} +2)^{2} +0+(2\sqrt{2} +1)^{2} } } = \arcsin \frac{-8-4\sqrt{2} }{\sqrt{625+440\sqrt{2} } \sqrt{21+12\sqrt{2} } } \approx \arcsin (-0.0628)\approx -0.06(rad)} \end{array}\]

\[\begin{array}{l} {\alpha _{4} =\arcsin \frac{\bar{l}_{4} \bar{n}_{4} }{\left|\bar{l}_{4} \right|\left|\bar{n}_{4} \right|} =\arcsin \frac{-2\sqrt{2}-2+0+(2\sqrt{2} +1)(2\sqrt{2} +2)}{\sqrt{1+(18+12\sqrt{2} )^{2} +(2+2\sqrt{2})^{2} } \sqrt{(2\sqrt{2} +2)^{2} +0+(2\sqrt{2} +1)^{2} } } = \arcsin \frac{8+4\sqrt{2} }{\sqrt{625+440\sqrt{2} } \sqrt{21+12\sqrt{2} } } \approx \arcsin (0.0628)\approx 0.06(rad)} \end{array}\]

Solution.

Let's build the figure D in the Cartesian coordinate system.

 

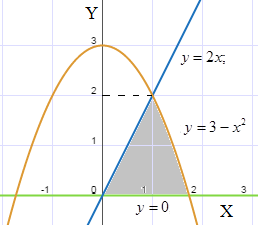
The bounds are:

\[0\le y\le 2;\frac{y}{2} \le x\le \sqrt{3-y} \]

The mass of the shaded cross-section:

\[\begin{array}{l} {M=\mathop{\int\!\!\!\!\int}\nolimits _{D}\mu (x,y)dxdy =\int _{0}^{2}dy \int _{y/2}^{\sqrt{3-y} }1\cdot dx =\int _{0}^{2}dy \int _{y/2}^{\sqrt{3-y} }dx =\int _{0}^{2}(\sqrt{3-y} -\frac{y}{2} )dy =-\frac{2}{3} \left. \sqrt{(3-y)^{3} } \right|_{0}^{2} -\left. \frac{y^{2} }{4} \right|_{0}^{2} =} \\ {=-\frac{2}{3} +\frac{2}{3} \sqrt{27} -1+0=2\sqrt{3} -\frac{2}{3} \approx 2.80(mass)} \end{array}\]

The coordinates of the center of gravity:

\[\begin{array}{l} {x_{C} =\frac{M_{x} }{M} =\frac{\mathop{\int\!\!\!\!\int}\nolimits _{D}xdxdy }{M} =\frac{\int _{0}^{2}dy \int _{y/2}^{\sqrt{3-y} }x\cdot dx }{M} =\frac{\int _{0}^{2}(3y-\frac{y^{2} }{4} )dy }{2M} =\frac{1}{2M} \left. (\frac{3y^{2} }{2} -\frac{y^{3} }{12} )\right|_{0}^{2} =} \\ {=\frac{1}{2M} (6-0-\frac{2}{3} +0)=\frac{5.3333}{5.6} \approx 0.95} \end{array}\] \[\begin{array}{l} {y_{C} =\frac{M_{y} }{M} =\frac{\mathop{\int\!\!\!\!\int}\nolimits _{D}ydxdy }{M} =\frac{\int _{0}^{2}ydy \int _{y/2}^{\sqrt{3-y} }dx }{M} =\frac{\int _{0}^{2}y(\sqrt{3-y} -\frac{y}{2} )dy }{M} =\frac{1}{M} ((-\left. \frac{y^{3} }{6} )\right|_{0}^{2} +\int _{0}^{2}y\sqrt{3-y} dy )=} \\ {=\frac{1}{M} (-\frac{4}{3} +0+\int _{0}^{2}y\sqrt{3-y} dy )=\left\{\begin{array}{c} {3-y=t^{2} } \\ {dy=-2tdt} \end{array}\right\}=-\frac{4}{3M} +\frac{1}{M} \int _{\sqrt{3} }^{1}(2t^{4} -6t^{2} )dt =} \\ {=-\frac{4}{3M} +\frac{1}{M} \left. (\frac{2t^{5} }{5} -2t^{3} )\right|_{\sqrt{3} }^{1} =-\frac{4}{3M} +\frac{1}{M} (\frac{2}{5} -2-\frac{18\sqrt{3} }{5} +6\sqrt{3} )=-\frac{4}{3M} -\frac{8}{5M} +\frac{12\sqrt{3} }{5M} =} \\ {=\frac{-44+36\sqrt{3} }{15M} \approx \frac{112.99}{42} \approx 0.44} \end{array}\]

Solution.

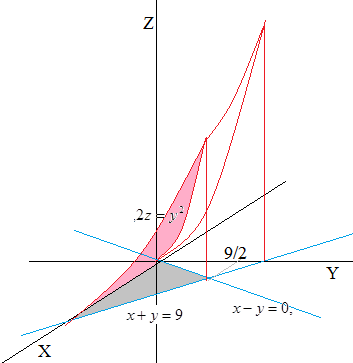
First we'll build the figure in the Cartesian coordinate system and will determine its bounds.

\[V:\left\{\begin{array}{c} {0\le y\le 9/2} \\ {y\le x\le 9-y} \\ {0\le z\le y^{2} /2} \end{array}\right. \]

Since the figure is uniform, we can determine the momentum of intertia I^z using the formula

\[\begin{array}{l} {I_{z} =\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits _{V}(x^{2} +y^{2} )dxdydz =\int _{0}^{9/2}dy \int _{y}^{9-y}dx \int _{0}^{y^{2} /2}(x^{2} +y^{2} )dz =\int _{0}^{9/2}dy \int _{y}^{9-y}dx\cdot \left. (x^{2} +y^{2} )z\right| _{0}^{y^{2} /2} =} \\ {=\int _{0}^{9/2}dy \int _{y}^{9-y}(x^{2} \frac{y^{2} }{2} +\frac{y^{4} }{2} )dx=\int _{0}^{9/2}dy \left. \left(\frac{y^{2} x^{3} }{6} +\frac{y^{5} x^{2} }{2} \right)\right|_{y}^{9-y} =} \\ {=\int _{0}^{9/2}(\frac{y^{2} (9-y)^{3} }{6} +\frac{y^{5} (9-y)^{2} }{2} -\frac{y^{5} }{6} -\frac{y^{7} }{2} )dy =} \\ {=\int _{0}^{9/2}(\frac{y^{2} (729-y^{3} +27y^{2} -243y)}{6} +\frac{y^{5} (81+y^{2} -18y)}{2} -\frac{y^{5} }{6} -\frac{y^{7} }{2} )dy =} \\ {=\int _{0}^{9/2}(\frac{729y^{2} -y^{5} +27y^{4} -243y^{3} }{6} +\frac{81y^{5} +y^{7} -18y^{6} }{2} -\frac{y^{5} }{6} -\frac{y^{7} }{2} )dy =} \\ {=\int _{0}^{9/2}(\frac{243y^{2} }{2} -\frac{121y^{5} }{3} +\frac{9y^{4} }{2} -\frac{81y^{3} }{2} +\frac{y^{7} }{2} -9y^{6} -\frac{y^{5} }{6} -\frac{y^{7} }{2} )dy =} \\ {=\int _{0}^{9/2}(\frac{243y^{2} }{2} -\frac{81y^{5} }{2} +\frac{9y^{4} }{2} -\frac{81y^{3} }{2} -9y^{6} )dy } \\ {=\left. \left(\frac{243\cdot y^{3} }{6} -\frac{81\cdot y^{6} }{6} +\frac{9\cdot y^{5} }{10} -\frac{81\cdot y^{4} }{8} -\frac{9y^{7} }{7} \right)\right|_{0}^{9/2} =} \\ {=\frac{81\cdot 91.125}{2} -\frac{27\cdot {\rm 8303,765625}}{2} +{\rm 1660,753125}-\frac{81\cdot {\rm 410,0625}}{8} -\frac{9\cdot {\rm 37366,9453125}}{7} =} \\ {={\rm 3690,5625-112100,8359375}+{\rm 1660,753125-4151,8828125-48043,215402}=} \\ {={\rm -158944,6185}} \end{array}\]

Solution.

Let's rewrite the equation of the plane in segments and build the pyramid. \[\frac{x}{4} +\frac{y}{-2} +\frac{z}{-4} =1\]

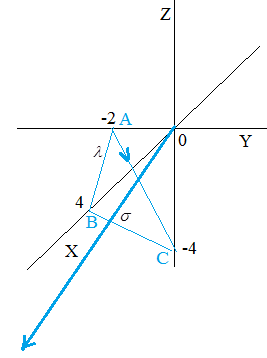
The normal to the plane (unit vector)

\[\bar{n}=(\frac{1}{4} \bar{i}-\frac{1}{2} \bar{j}-\frac{1}{4} \bar{k})/(\sqrt{3} /2\sqrt{2} )=\frac{\sqrt{2} }{2\sqrt{3} } \bar{i}-\frac{\sqrt{2} }{\sqrt{3} } \bar{j}-\frac{\sqrt{2} }{2\sqrt{3} } \bar{k}\]

a) Let's find the immediate flux of the vector field through the surfuce.

\[\frac{x}{4} +\frac{y}{-2} +\frac{z}{-4} =1\] \[\bar{n}=(\frac{1}{4} \bar{i}-\frac{1}{2} \bar{j}-\frac{1}{4} \bar{k})/(\sqrt{3} /2\sqrt{2} )=\frac{\sqrt{2} }{2\sqrt{3} } \bar{i}-\frac{\sqrt{2} }{\sqrt{3} } \bar{j}-\frac{\sqrt{2} }{2\sqrt{3} } \bar{k}\] \[z=-4+x-2y;\quad z'_{x} =1;z'_{y} =-2\] \[\begin{array}{l} {{\rm \; }\Phi _{p} {\rm (}\bar{{\rm F}}{\rm )=}\mathop{\int\!\!\!\!\int}\nolimits _{\sigma }\bar{{\rm F}}\cdot \bar{n}ds =\mathop{\int\!\!\!\!\int}\nolimits _{p}\frac{\sqrt{2} }{2\sqrt{3} } (y-x+z)ds =\frac{\sqrt{2} }{2\sqrt{3} } \mathop{\int\!\!\!\!\int}\nolimits _{p}(y-x+z)ds =} \\ {=\frac{\sqrt{2} }{2\sqrt{3} } \int _{-2}^{0}dx \int _{\frac{1}{2} x-2}^{0}(y-x+z)\cdot \sqrt{1+(z'_{x} )^{2} +(z'_{y} )^{2} } dy=\frac{\sqrt{2} }{2\sqrt{3} } \int _{-2}^{0}dx \int _{\frac{1}{2} x-2}^{0}(y-x-4+x-2y)\cdot \sqrt{6} dy=} \\ {=\int _{-2}^{0}dx \int _{\frac{1}{2} x-2}^{0}(-y-4) dy=\int _{-2}^{0}dx \cdot \left. (-\frac{y^{2} }{2} -4y)\right|_{\frac{1}{2} x-2}^{0} =\int _{-2}^{0}dx \cdot (0+\frac{(\frac{1}{2} x-2)^{2} }{2} +4(\frac{1}{2} x-2))=} \\ {=\int _{-2}^{0}(\frac{x^{2} }{4} -x+2+2x-8)dx =\int _{-2}^{0}(\frac{x^{2} }{4} +x-6)dx =\left. \left(\frac{x^{3} }{12} -6x+\frac{x^{2} }{2} \right)\right|_{-2}^{0} =0-(\frac{-8}{12} +12+2)=-\frac{40}{3} } \end{array}\]

b) Let's find the immediate flux of the vector field

$$\bar{F}=(y-x+z)\bar{i}$$ through the surface $$S1:z=0$$ Normal (orth) $$\bar{n}=(0,0,-1)$$ \[\Phi _{s1} (\bar{F})=\mathop{\int\!\!\!\!\int}\nolimits _{S1}\bar{F}\cdot \bar{n}ds =-\mathop{\int\!\!\!\!\int}\nolimits _{s1}0ds =0\]

c) Let's find the immediate flux of the vector field through the surfuce $$S2:x=0$$

Normal (orth) $$\bar{n}=(-1,0,0)$$ \[\begin{array}{l} {{\rm \; }\Phi _{S2} {\rm (}\bar{{\rm F}}{\rm )=}\mathop{\int\!\!\!\!\int}\nolimits _{S2}\bar{{\rm F}}\cdot \bar{n}ds =-\mathop{\int\!\!\!\!\int}\nolimits _{S2}(y-x+z)ds =-\int _{-2}^{0}dy \int _{-4-2y}^{0}(y+z)dz =-\int _{-2}^{0}dy \left. (yz+\frac{z^{2} }{2} )\right|_{-4-2y}^{0} =} \\ {=-\int _{-2}^{0}\left(0-y(-4-2y)-\frac{1}{2} (-4-2y)^{2} \right)dy =-\int _{-2}^{0}\left(+4y+2y^{2} -2(4+4y+y^{2} )\right)dy =} \\ {=-\int _{-2}^{0}\left(4y+2y^{2} -8-8y-2y^{2} \right)dy =-\int _{-2}^{0}\left(-4y-8\right)dy =\int _{-2}^{0}\left(4y+8\right)dy =\left. (2y^{2} +8y)\right|_{-2}^{0} =} \\ {=0-(8-16)=8} \end{array}\]

d) Let's find the immediate flux of the vector field through the surfuce $$S3:y=0$$ \[\bar{n}=(0,-1,0)\] \[\Phi _{s3} (\bar{F})=\mathop{\int\!\!\!\!\int}\nolimits _{S3}\bar{F}\cdot \bar{n}ds =\mathop{\int\!\!\!\!\int}\nolimits _{s3}0ds =0\] In order to find the calculated flux through the enclosed surface σ, let's use the ratio \[\Phi _{\sigma } (\bar{F})=\Phi _{s1} (\bar{F})+\Phi _{s2} (\bar{F})+\Phi _{s3} (\bar{F})+\Phi _{p} (\bar{F})=0+8+0-\frac{40}{3} =\frac{24-40}{3} =-\frac{16}{3} \] Field components: \[\begin{array}{l} {P=y-x+z;\quad \frac{\partial P}{\partial x} =-1;\frac{\partial P}{\partial y} =1;\frac{\partial P}{\partial z} =1} \\ {Q=0;\; \frac{\partial Q}{\partial y} =0;\quad R=0;\quad \frac{\partial R}{\partial z} =0} \end{array}\] Divergence $$div\bar{F}=\frac{\partial P}{\partial x} +\frac{\partial Q}{\partial y} +\frac{\partial R}{\partial z} =-1$$ \[\frac{\partial R}{\partial y} -\frac{\partial Q}{\partial z} =0;\frac{\partial P}{\partial z} -\frac{\partial R}{\partial x} =1;\frac{\partial Q}{\partial x} -\frac{\partial P}{\partial y} =-1\] Curl $$curl\bar{F}=\bar{j}-\bar{k}$$

The flux of the vector field over the entire surface using Ostrogradskii's formula

$$\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits _{V}div\bar{F}dxdydz =-\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits _{V}1\cdot dxdydz =-\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits _{V}dxdydz =-V_{OABC} =-\frac{1}{3} \cdot \frac{1}{2} \cdot 2\cdot 4\cdot 4=-\frac{16}{3} $$

Circulation of the vector field F on the contour λ equals the linear integral

\[\oint _{\lambda }\bar{F}d\bar{r} =\oint _{\lambda }(F_{x} dx+F_{y} dy+F_{z} dz)= \oint _{\lambda }(y-x+z)dx \] \[\begin{array}{l} {\lambda _{1} :y=\frac{1}{2} x-2;z=0\quad ;dy=\frac{dx}{2} ;dz=0;\quad x_{1} =4;x_{2} =0} \\ {\lambda _{2} :z=x-4;dz=dx;y=0;dy=0;0\le x\le 4} \\ {\lambda _{3} :z=-2y-4;dz=-2dy;x=0;dx=0;-2\le y\le 0} \end{array}\] \[\begin{array}{l} {\oint _{\lambda }(y-x+z)dx =\int _{\lambda _{1} }(y-x+z)dx +\int _{\lambda _{2} }(y-x+z)dx +\int _{\lambda _{3} }(y-x+z)dx =} \\ {=\int _{4}^{0}(\frac{1}{2} x-2-x+0)dx +\int _{0}^{4}(0-x+x-4)dx +0=} \\ {=\int _{4}^{0}(-\frac{1}{2} x-2)dx -4\int _{0}^{4}dx =\frac{1}{2} \int _{0}^{4}(x+4)dx -4\int _{0}^{4}dx =\frac{1}{2} \left. \left(\frac{x^{2} }{2} +4x\right)\right|_{0}^{4} -16=} \\ {=\frac{1}{2} (8+16)-16=12-16=-4} \end{array}\]

Normal to the plane (unit vector)

\[\bar{n}=(\frac{1}{4} \bar{i}-\frac{1}{2} \bar{j}-\frac{1}{4} \bar{k})/(\sqrt{3} /2\sqrt{2} )=\frac{\sqrt{2} }{2\sqrt{3} } \bar{i}-\frac{\sqrt{2} }{\sqrt{3} } \bar{j}-\frac{\sqrt{2} }{2\sqrt{3} } \bar{k}\] \[curl\bar{F}=\bar{j}-\bar{k}\]

Using Stokes' theorem:

\[\mathop{\int\!\!\!\!\int}\nolimits _{\sigma }\bar{n}curl\bar{F}d\sigma = \mathop{\int\!\!\!\!\int}\nolimits _{\sigma }(\bar{j}-\bar{k})(\frac{\sqrt{2} }{2\sqrt{3} } \bar{i}-\frac{\sqrt{2} }{\sqrt{3} } \bar{j}-\frac{\sqrt{2} }{2\sqrt{3} } \bar{k})d\sigma = \mathop{\int\!\!\!\!\int}\nolimits _{\sigma }(-\frac{\sqrt{2} }{\sqrt{3} } +\frac{\sqrt{2} }{2\sqrt{3} } )d\sigma =-\frac{\sqrt{2} }{2\sqrt{3} } S_{\sigma } \]

The flat figure σ is an isoscles triangle ABC with sides:

\[AB=\sqrt{2^{2} +4^{2} } =\sqrt{20} =2\sqrt{5} ;\quad BC=4\sqrt{2} ;\quad AC=\sqrt{2^{2} +4^{2} } =\sqrt{20} =2\sqrt{5} . \] Then the height $$h=\sqrt{20-8} =\sqrt{12} =2\sqrt{3} $$ $$S_{\sigma } =\frac{1}{2} BC\cdot h=\frac{1}{2} 4\sqrt{2} \cdot 2\sqrt{3} =4\sqrt{6} $$ \[-\frac{\sqrt{2} }{2\sqrt{3} } S_{\sigma } =-\frac{\sqrt{2} }{2\sqrt{3} } \cdot 4\sqrt{6} =-4\]